2ème partie–Deferred Rendering et les lumières

Introduction

 

Dans la première partie de cet article, nous avons introduit le Deferred Rendering, commencé à le mettre en place avec le Framework XNA 4.0, et dessiner notre premier objet avec tous ces attributs dans le G-Buffer. Passons immédiatement à la suite, avec la mise en place des différents type de lumière dans un moteur de Deferred Rendering !

Lumières !

 

Avant d’attaquer le gros de cette partie, faisons un peu de théorie sur la lumière.

En 3D, le calcul de la lumière nécessite 3 composantes : une composante dite diffuse, une composante dite spéculaire, et une composante dite ambiante. La composante diffuse permet de nuancer la lumière suivant l’inclinaison d’une surface par rapport à la lumière. La composante spéculaire permet de rajouter un point de brillance pour modifier le rendu des objets à l’écran. Enfin, la composante ambiante permet de simuler très approximativement les rayons lumineux qui se réfléchissent sur les surfaces et qui font qu’une ombre n’est pas noire, mais grise foncée.

Au lieu de réinventer la roue, je vous renvoie vers ces deux articles Wikipedia qui expliquent le fonctionnement du modèle d’ombrage de Phong, qui est celui le plus utilisé (et le plus simple) en simulation de lumière :

http://fr.wikipedia.org/wiki/Ombrage_Phong

http://en.wikipedia.org/wiki/Blinn%E2%80%93Phong_shading_model

Remarque : C’est le modèle Blinn-Phong que nous utilisons. En effet, son calcul de la lumière spéculaire est plus performant, ce qui permet d’économiser quelques instructions pour un résultat quasi-identique.

 

Les lumières directionnelles

Passons maintenant à la mise en pratique de cette partie théorique. Les lumières directionnelles sont les plus simples à simuler. Ce sont des lumières comme celle du soleil par exemple, c’est à dire qu’elles sont représentées uniquement par une direction. Dans le cas du Deferred Rendering, on calcule la lumière pour chaque pixel de notre scène, et l’on dessine le résultat sur un nouveau RenderTarget. Si l’on reprend notre équation N.L (ici, le . veut dire que l’on calcule le produit scalaire des deux vecteurs), cette direction correspond au vecteur L. Mais comment obtenir le vecteur N ? Et bien, c’est simple. Dans la première partie de cet article, nous avons utilisé un RenderTarget qui contient la normale de chaque pixel. Il nous suffit dans un PixelShader de récupérer cette normale, et d’appliquer l’équation dont on inscrira le résultat le nouveau RenderTarget. Voici l’extrait du PixelShader permettant de calculer la normale et la lumière pour chaque pixel de la scène :

 

1. float4 DirectionalPS(VStoPS IN): COLOR0
2. {
3.     // Get Normal
4.     float3 normal = float3(tex2D(NormalSampler, IN.TexCoord).xy, 0);
5.     normal.z = sqrt(1 – (normal.r * normal.r) – (normal.g * normal.g));
6.  
7.     // Get View Position
8.     float depth = tex2D(DepthSampler, IN.TexCoord).x;
9.     float3 viewRay = IN.PosVS.xyz;
10.     float3 position = viewRay * depth;
11.  
12.     // Diffuse Light
13.     float nDotL = dot(normal, -LightDirection);
14.     float3 DiffuseLight = max(nDotL, 0) * LightColor;
15.  
16.     // Specular
17.     float3 viewDir = normalize(-position);
18.     float3 halfVec = normalize(viewDir – LightDirection);   
19.     float nDotH = saturate(dot(normal, halfVec));       
20.     float SpecularLight = pow(nDotH, 50.0) * 1.0 * nDotL;   
21.  
22.     returnfloat4(DiffuseLight.r, DiffuseLight.g, DiffuseLight.b, SpecularLight);
23. }

 

Bien, expliquons ce qui se passe. Premièrement, on récupère la normale. Comme expliqué dans la première partie de l’article, nous avons fait le choix d’utiliser une surface contenant deux float de 16 bits pour sauvegarder la normale, ce qui nous permet de gagner en précision. Mais il nous manque le Z de cette normale ! Mais pas de panique, vu que chaque normale est normalisée (de longueur égale à 1), nous pouvons retrouver le Z de cette avec l’équation z = SQRT(1 – x*x – y*y) (sqrt étant la racine carrée). Ce que nous faisons ici en HLSL, et ce qui nous permet au final de bien avoir notre normale.

Ensuite nous récupérons la position du pixel dans le view space. Pour cela, nous avons besoin de la profondeur du pixel (contenue dans le DepthRenderTarget de la première partie). Mais il nous manque le X et le Y de la position. Mais ça tombe bien, puisque dans mon VertexShader, j’ai calculé la position de mon quad (que je me sers pour dessiner une texture à l’écran, la classe QuadRenderer) dans le view space. J’obtiens donc un vecteur normalisé dans la direction de mon pixel. Nous avons alors plus qu’à le multiplier par la profondeur du pixel, et nous obtenons la position du pixel dans l’espace. Magique .

 

Ensuite, nous retrouvons la composante diffuse de la lumière calculée avec la formule N.L. Nous multiplions l’intensité de la lumière obtenons par la couleur de la lumière (imaginez un soleil bleu par exemple, et bien, c’est ici qu’on le rend bleu ), et nous retournerons ce résultat dans le RenderTarget dédié à la lumière.

Et ensuite vient le calcul de la composante spéculaire de la lumière. D’après l’équation, nous avons besoin du vecteur normal de la surface ( N ), et d’un vecteur H, qui est la différence entre le vecteur de vue (le vecteur qui va du pixel en cours de calcul jusqu’à la caméra, c’est à dire votre oeil) et le vecteur directeur de la lumière. Une fois l’intensité spéculaire obtenue, nous pouvons la nuancer à l’aide d’une fonction de puissance. Augmenter cette puissance donnera l’illusion d’une surface très brillante, la diminuer donnera l’illusion d’une surface plus matte. Aussi, nous pouvons multiplier cette intensité pour l’intensité diffuse pour que le résultat visuel soit plus cohérent (évite les surplus de brillance dans des zones qui devraient être sombres).

Ensuite on retourne le tout sous forme de couleur dans un le RT de la lumière, avec la couleur de la lumière diffuse en R, G et B, et l’intensité spéculaire en A.

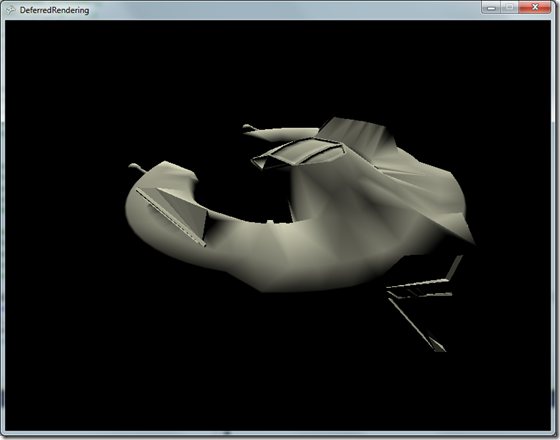
Au final, le calcul de la lumière directionnelle donne cette image :

 

Il ne nous reste plus qu’à mélanger le tout pour obtenir notre image finale.

Pour cela nous écrivons un shader particulier (encore un oui ) qui retournerons le résultat dans un (encore) nouveau RenderTarget. Si vous avez bien suivi, vous remarquerez qu’il y a un des RT du GBuffer qui n’a pas été utilisé : celui qui contient les données de couleur de chaque pixel. Et bien il va servir ici, et mélangé à la lumière, nous aurons donc notre scène finale ! Ci-dessous se trouve le shader de composition de l’image finale :

 

1. float4 CompositePS(VStoPS IN) : COLOR0
2. {
3.     float4 OUT;
4.  
5.     float4 diffuseColor = tex2D(ColorSampler, IN.TexCoord);
6.     float4 light = tex2D(LightSampler, IN.TexCoord);
7.  
8.     // get diffuse
9.     float3 diffuseLight = light.rgb;
10.  
11.     // get specular
12.     float specular = light.a;
13.  
14.     // compute final color
15.     OUT = float4((diffuseLight + specular + (AmbiantColor.rgb * 0.1)) * diffuseColor.rgb, 1);
16.     return OUT;
17. }

 

Bien, expliquons ce bout de code. Les deux premières lignes n’ont rien d’exceptionnel, on récupère d’abord la couleur du pixel, puis l’intensité de la lumière qui lui est appliqué. Ensuite, pour plus de lisibilité, on récupère dans un vecteur 3D la lumière diffuse, puis dans un float la lumière spéculaire. Et enfin, nous retournons sous forme de vecteur 4D le pixel correct, c’est à dire que l’on additionne les 3 composantes de la lumière ensemble, puis on multiplie cette somme à la couleur du pixel. Et TADA ! Nous avons un beau vaisseau tout éclairé (case en haut à droite ) :

 

 

 

Les lumières omnidirectionnelles

Le monde réel n’est pas fait uniquement de lumière du soleil. On trouve aussi des lumières à l’intérieur, émises par une ampoule, une télévision allumée, etc… Ces lumières là sont des lumières ponctuelles, qui émettent dans toutes les directions et qui s’atténuent avec la distance. C’est ce qu’on appelle une lumière omnidirectionnelle. Les calculs de ce type de lumière ne change pas fondamentalement, mais il faut maintenant savoir situer la lumière dans l’espace et calculer la distance entre cette lumière et la surface illuminée. Voici le PixelShader permettant de faire ça :

 

1. float4 PointLightPS(VStoPS IN) : COLOR0
2. {
3.     IN.PosCS.xy = IN.PosCS.xy / IN.PosCS.w;
4.     float2 texCoord = 0.5f * ( float2(IN.PosCS.x,-IN.PosCS.y) + 1);
5.     texCoord -= HalfPixel;
6.  
7.     // Get Normal
8.     float3 normal = float3(tex2D(NormalSampler, texCoord).xy, 0);
9.     normal.z = sqrt(1 – (normal.r * normal.r) – (normal.g * normal.g));
10.  
11.     // Get View Position
12.     float depth = tex2D(DepthSampler, texCoord).x;
13.     float3 viewRay = IN.PosVS.xyz * (FarPlane / -IN.PosVS.z);
14.     float3 position = viewRay * depth;
15.  
16.     // Diffuse Light   
17.     float3 lightDirection = position – LightPositionVS;
18.     float attenuation = max(0, (Radius – length(lightDirection)) / Radius);
19.     lightDirection = normalize(lightDirection);
20.     float nDotL = dot(normal, -lightDirection) * attenuation;
21.     float3 DiffuseLight = max(nDotL, 0) * LightColor;
22.  
23.     // Specular
24.     float3 viewDir = normalize(-position);
25.     float3 halfVec = normalize(viewDir – lightDirection);   
26.     float nDotH = saturate(dot(normal, halfVec));       
27.     float SpecularLight = pow(nDotH, 50.0) * 1.0 * nDotL;
28.  
29.     returnfloat4(DiffuseLight.r, DiffuseLight.g, DiffuseLight.b, SpecularLight);
30. }

 

Peu de changement ici, mais regardons de plus près le calcul de la position et celui de la lumière diffuse.

Ici, nous ne dessinons pas la lumière à l’aide du QuadRenderer (cf. lumière directionnelle), mais nous dessinons une sphère en 3D qui représente la lumière omnidirectionnelle (ce qui permet par ailleurs d’optimiser et de rendre plus performant le calcul de ce genre de lumière, puisque seulement les pixels touchés par la sphère vont être impactés). Donc pour retrouver la position du pixel, ça devient un peu plus compliqué, mais pas tant que ça. Ici, PosVS contient la position dans le viewSpace du pixel en cours de calcul. Sauf que ce pixel se trouve sur la sphère, et pas sur le FarPlane de la caméra. Et du coup il nous faut projeter ce pixel sur le FarPlane. Rien de plus simple, il suffit d’appliquer un coefficient à la position du pixel. Ce coefficient ce calcul de la façon suivante : c’est le rapport entre le FarPlane de la caméra, et le négatif de la profondeur du pixel en cours. On multiplie ensuite ce coefficient à la position, et nous voilà projeter sur le FarPlane avec un vecteur exploitable pour calculer la position du pixel dans le ViewSpace.

Ensuite, nous calculons la lumière diffuse. Ici, la direction de la lumière n’est pas la même pour chaque pixel, il faut donc la calculer. Pour cela, nous utilisons une petite soustraction entre la position de la lumière et la position du pixel courant. Ensuite, nous calculons l’atténuation de ce pixel dû à la distance. Pour cela, nous divisons la distance entre le pixel et la lumière par la distance d’émission de la lumière. Ce qui nous donne un nombre entre 0 et 1, très pratique pour nuancer l’intensité lumineuse. Et ensuite le calcul est le même que pour la lumière directionnelle, sauf que l’intensité lumineuse de la lumière diffuse est multiplié par le rapport de la distance.

Vu que nous faisons du Deferred Rendering, nous allons utiliser sa flexibilité pour dessiner pas moins de 20 lumières en même temps, ce qui donne ceci au niveau du RT de la lumière (la lumière directionnelle n’est pas présente ici) :

 

Et ceci en image finale :

Plutôt cool, hein ?

 

Les lumières spot

Les lumières spot sont les dernières lumières à être traitées. Ce sont simplement des spots, donc semblable aux lumières omnidirectionnelles dans un sens, et directionnelles dans l’autre. Mais en plus de ça, il faut aussi prendre en compte l’estompage du disque de lumière avec l’ombre. Voici le code shader qui permet de dessiner une lumière de type spot :

1. float4 SpotLightPS(VStoPS IN) : COLOR0
2. {
3.     IN.PosCS.xy = IN.PosCS.xy / IN.PosCS.w;
4.     float2 texCoord = 0.5f * ( float2(IN.PosCS.x,-IN.PosCS.y) + 1);
5.     texCoord += HalfPixel;
6.  
7.     // Get Normal
8.     float3 normal = 2.0 * tex2D(NormalSampler, texCoord).xyz – 1.0;
9.  
10.     // Get View Position
11.     float depth = tex2D(DepthSampler, texCoord).x;
12.     float3 viewRay = IN.PosVS.xyz * (FarPlane / -IN.PosVS.z);
13.     float3 position = viewRay * depth;
14.  
15.     // Diffuse Light   
16.     float3 lightDirection = position – LightPositionVS;
17.     floatdistance = length(lightDirection);
18.     lightDirection = normalize(lightDirection);
19.     float spotDotLight = dot(lightDirection, DirectionVS);
20.     float attenuation = 1/( 0.03 + 0.01 * distance + 0.006 * distance * distance);
21.  
22.     float spotIntensity = 0;   
23.     if(spotDotLight > InnerCone)
24.         spotIntensity = 1;
25.     elseif(spotDotLight <= OuterCone)
26.         spotIntensity = 0;
27.     else
28.         spotIntensity = pow( (spotDotLight – OuterCone) / (InnerCone – OuterCone), 3);
29.    
30.     float nDotL = dot(normal, -lightDirection) * spotIntensity * attenuation;
31.     float3 DiffuseLight = max(nDotL, 0) * LightColor;
32.  
33.     // Specular
34.     float3 viewDir = normalize(CameraPositionVS – position);
35.     float3 halfVec = normalize(viewDir – lightDirection);   
36.     float nDotH = saturate(dot(normal, halfVec));   
37.    
38.     float SpecularLight = pow(nDotH, 50.0) * 1.0 * nDotL;
39.  
40.     returnfloat4(DiffuseLight.r, DiffuseLight.g, DiffuseLight.b, SpecularLight);
41. }

 

Un peu plus compliqué cette fois. Une fois de plus, c’est le calcul de la composante diffuse de la lumière qui gagne en complexité. Tout commence comme pour une lumière omnidirectionnelle, sauf que deux variables apparaissent en plus : spotDotLight et spotIntensity . La première variable permet de savoir l’angle entre la direction centrale de la lumière et le vecteur directeur du pixel jusqu’à la lumière. Ensuite, nous calculons l’atténuation par rapport à la distance de la lumière. La deuxième variable, spotEntensity, permet en fait de calculer l’atténuation de la lumière par rapport au centre du spot, pour effectuer en passage en douceur vers la pénombre. Cette intensité se calcule en comparant l’angle spotDotLight à deux valeurs seuils : InnerCone, qui représente le seuil d’angle interne du spot à partir duquel il faudra commencer à atténuer la lumière, et OuterCone qui représente le seuil d’angle à partir duquel il n’y aura plus aucune atténuation et où on sera dans l’ombre totale. Donc suivant où se situe l’angle courant, on affectera l’intensité en fonction : intensité maximale si l’angle est inférieur à InnerCone, intensité nulle si l’angle est supérieur à OuterCone, et nuancé avec atténuation si on est entre InnerCone et OuterCone. Ensuite on calcule l’intensité diffuse globale ajoutant ici la multiplication avec spotIntensity.

Conclusion

 

Améliorations

Nous avons ici un moteur de rendu différé fonctionnel qui permet d’afficher de nombreuses lumières en même temps sans grosses pertes de performances. Néanmoins plusieurs points restes à améliorer :

– Optimiser le code et les performances

– Ajouter le support des objets transparents. En effet, il n’est pas possible avec le Deferred Rendering de dessiner des objets transparents. On pourrait imaginer dessiner ces objets transparents dans un renderer classique, puis cet RT au rendu différé.

– Palier le manque de MSAA. En effet, l’antialising matériel n’est plus fonctionnel avec le Deferred Rendering. On pourrait imaginer mettre en place une solution software, c’est à dire un effet de post processing qui s’occuperait d’appliquer un flou sur les arrêtes des objets (arrêtes détectés à l’aide des normales et de la profondeur)

– Support des matériaux

 

Conclusion

Dans cet article, nous avons quels sont les avantages et inconvénients du Deferred Rendering et comment dessiner tout type de lumière de façon performante. Vous trouverez ci-dessous les sources qui m’ont inspiré pour cet article ainsi que le code source du projet.

Sources

 

Sources

Catalin Zima, http://www.catalinzima.com/tutorials/deferred-rendering-in-xna/

Shawn Hargreaves, http://http.download.nvidia.com/developer/presentations/2004/6800_Leagues/6800_Leagues_Deferred_Shading.pdf

Crytek, http://www.crytek.com/sites/default/files/A_bit_more_deferred_-_CryEngine3.ppt

Wikipedia, http://en.wikipedia.org/wiki/Deferred_shading

Killzone 2, http://www.guerrilla-games.com/publications/dr_kz2_rsx_dev07.pdf

Publicité